What is Radioactive Decay?
Radioactive decay is a spontaneous nuclear transformation that has been shown to be unaffected by pressure, temperature, chemical form, etc (except a few very special cases). Radioactive decay involves a transition from a definite quantum state of the original nuclide to a definite quantum state of the product nuclide. Example of α decay-
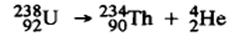
This process of transforming one element to another is known as transmutation.
Types of Radioactive decay
Radioactive decay is of five types
i. Alpha Emission
ii. Beta Emission
iii. Gamma Emission
iv. Positron Emission
v. Electron Capture
Decay Energy
The energy difference between the two quantum levels involved in the transition corresponds to the decay energy. This decay energy appears in the form of electromagnetic radiation and as the kinetic energy of the products.
Radioactivity: Emission of radiation during radioactive decay is called Radioactivity.
Types:
i. Natural Radioactivity
ii. Artificial Radioactivity
The SI unit of radioactivity is Becqueral (Bq). 1 Bq= 1 dps (disintegrations per second) Previously Curie (Ci) is widely used. 1 Ci = 3.7 X 1010 dps.
i. Alpha Emission: Emission of α particles ( 42He nucleus) is observed for the elements heavier than lead and for a few nuclei as light as the lanthanide elements. It can be written symbolically as
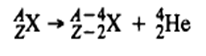
We use X to indicate any element defined by its nuclear charge, Z and Z-2 in this equation. e.g.
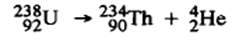
ii. Beta Emission: Emission of a high speed electron ( 0-1e) from radionuclides. Generally it is written as-
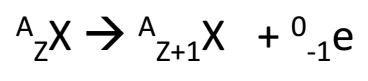
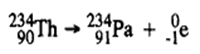
III. Positron Emission: Emission of a positron ( 01e) from radionuclides.
General representation-
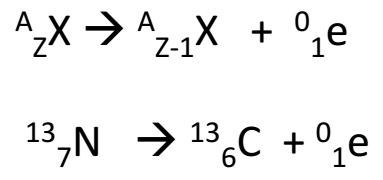
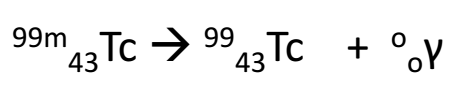
IV. Gamma Emission: Emission of a gamma photon from an radionuclides
V. Electron capture is a process in which a proton-rich nuclide absorbs an inner atomic electron, thereby changing a nuclear proton to a neutron and simultaneously causing the emission of an electron neutrino. Various photon emissions follow, as the energy of the atom falls to the ground state of the new nuclide. It is sometimes called inverse beta decay.
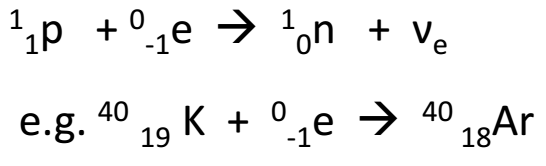
Kinetics of Radioactive Decay
Radioactive decay is a first-order reaction; that is, the rate of radioactive decay is proportional to the number of each type of radioactive nuclei present in a given sample. So, if we double the number of a given type of radioactive nuclei in a sample, we double the number of particles emitted by the sample per unit time. The relation may be expressed as-
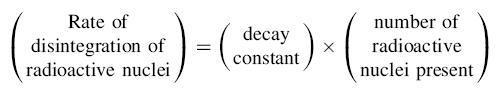
Let N represent the number of radioactive nuclei present at time t. Then, using differential calculus, the preceding word equations may be written as-
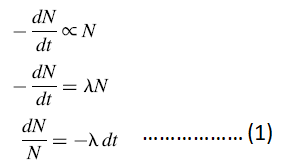
If we say that at time t = 0 we have N0 radioactive nuclei present, then integration of Equation (1) gives the radioactive decay law

it is easy to show that the counting rate in one’s radiation detector, C, is equal to the rate of disintegration of the radioactive nuclei present in a sample, A, multiplied by a constant related to the efficiency of the radiation measuring
system. Thus
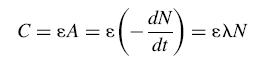
where epsilon is the efficiency. Substituting into Equation (2), we get
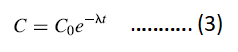
Where C is the counting rate at some time t due to a radioactive sample that gave counting rate C0 at time t = 0.
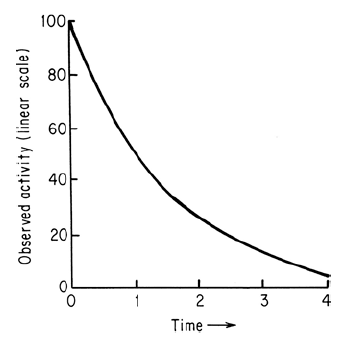
Half-life of Radioactive Decay
The half-life (t1/2) is another representation of the decay constant. The half-life of a radionuclide is the time required for its activity to decrease by exactly one-half. Thus, after one half-life, 50% of the initial activity remains. After two half-lives, only 25% of the initial activity remains. After three half-lives, only 12.5% is yet present and so forth. Figure below shows this relation graphically. The half-life for a given nuclide can be derived from Equation (2) when the value of the decay constant is known. In accordance with the definition of the term half-life, when N = N0/2 then t = t1/2. Substituting these values into Equation (2) gives
N0/2 = N0 e–λt1/2
½ = e–λt1/2
ln ½ = ln e–λt1/2
0.693 = λ t1/2
t1/2 = 0.693/λ
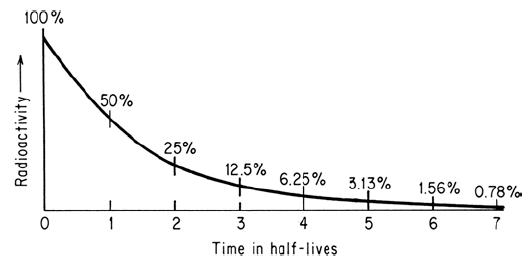
Problem: Given the data plotted below for the decay of a single radionuclide, determine the decay constant and the half-life of the nuclide.
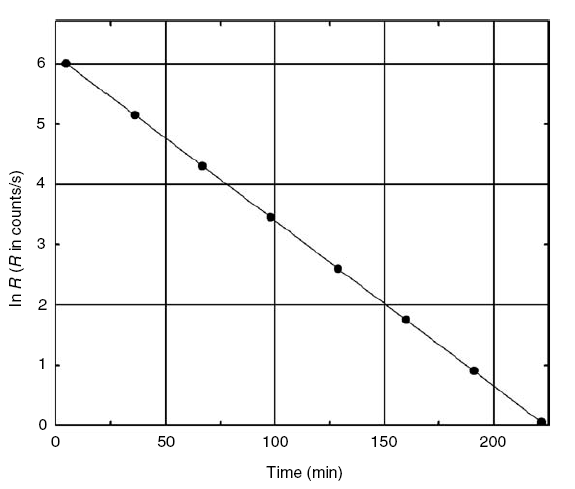
Solution: Slope of the graph equals to the decay constant.
Slope = (6:06 – 0)/(220 min-0)
= 0.0275 min-1
So, λ = 0.0275 min-1
t1/2 = o.693/ 0.0275 min-1
= 25.2 min
Although the half-life of a given radionuclide is a defined value, the actual moment of disintegration for a particular atom can be anywhere from the very beginning of the nuclide’s life to infinity. The average or mean life of a population of nuclei can be calculated. The mean life t is naturally related to the decay constant and is, in fact, simply the reciprocal of the decay constant:
τ = 1/λ
or the mean life can be expressed in terms of the half-life:
τ = 1.443 t1/2
Difference between activity and specific activity
The activity of a certain sample is the number of a radioactive disintegrations per second. The specific activity is defined as the number of disintegrations per unit weight or volume of sample.
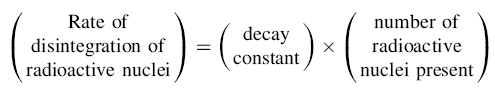
We can write this equation as:
A = λN where A = Activity
we know, N = N0e –λt so, A = A0e –λt ………………..(5)
The activity of a certain sample is the number of a radioactive disintegrations per second. The specific activity is defined as the number of disintegrations per unit weight or volume of sample.
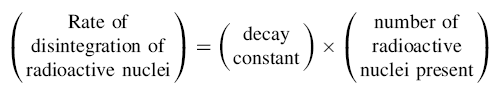
We can write this equation as:
A = λN where A = Activity
So, Specific activity Aspec = λ N/G , where, G = weight or volume of sample
Problem: Calculate the specific tritium (3H) activity of 3 liter water containing one 3H atom per 1018 hydrogen atoms. Given that T1/2 = 12.43 years.
Solution: We know
Aspec = λ N/G
Here, λ = 0.693/ (12.43 x 365 x 24 x 60 x 60) = 391992480 = 0.00000000177 s-1
Molar mass of water M = 18.0 g/mole
No of moles of water in 3 litre = 3000/18 moles = 166.67
G = 3000 mL
N = 2 x 10-18 x 166.67 x 6.023 x 1023 = 200770682
N/G = 66923.56
So, Aspec = 0.00000000177 s-1 x 66923.56 = 0.00011845 Bq/mL
or, = 0.1184 Bq/L
Growth of Radioactive Products in a Decay Chain
Before discussing growth of radioactive products in a decay chain we can restrict ourselves to the relation between a parent and a daughter activity.
We can write
A ……λ1………>B…… λ1 ………> C (stable)
we know, N = N0e –λt and A = λN where A = Activity
so, A = A0e –λt ……………………………(5)

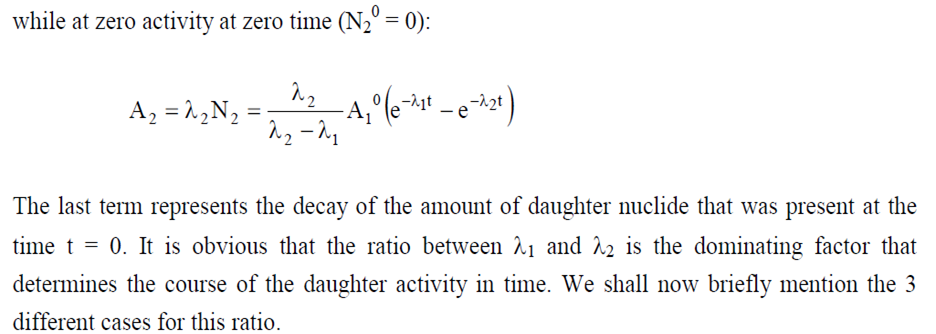
λ1< < λ2 : Secular Equilibrium
λ1< λ2 : Transient Equilibrium
λ1 ˃ λ2 : No Equilibrium
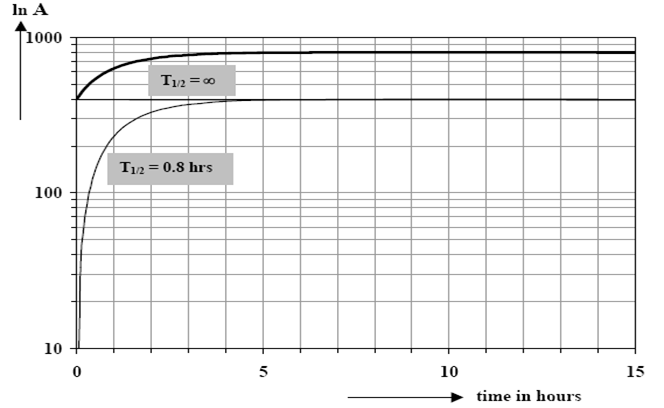
Secular Equilibrium
When the half-life of the parent nuclide is infinitely larger than that of the daughter nuclide secular equilibrium occurs. Examples are the relations between the long-living isotopes of uranium and thorium, 238U, 235U and 232Th, and their decay products.
when λ1< < λ2
Eq. (5) properly describes the parent activity in time, whereas Eq. (7) turns into:
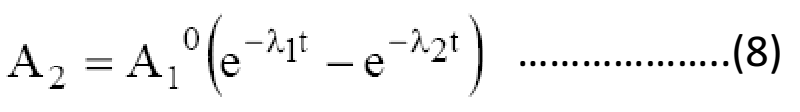
Since λ1 is very small so e –λ1t ≈ 1 and Eq. (8) becomes-
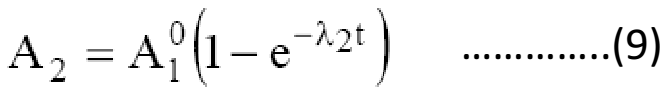
At t→∞ at e –λ2t ≈ 0 , so Eq. (9) stands-
A2 = A1
i.e. Parents and daughter activity become equal
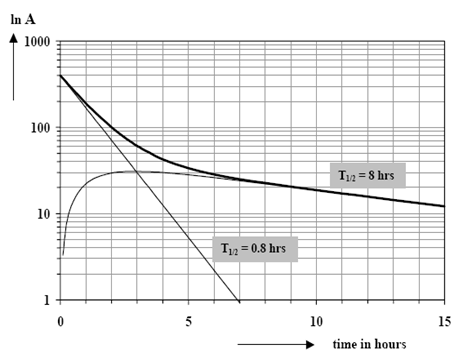
Transient Equilibrium
In this case, the half-life of the parent nuclide is still larger than that of the daughter nuclide but not infinitely: i.e λ1< λ2. so, there is a measureable decay of the parent during the experiment. Under this condition e –λ2t in Eq. 7 is negligible
Growth of the daughter after zero activity at zero time now occurs according to Eq. 7. A stationary state is reached after sufficient time in which the daughter activity is larger than the parent activity, as is to be expected. Fig. shows the course of both activities:
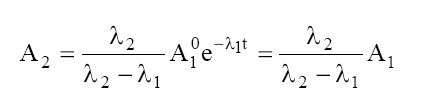
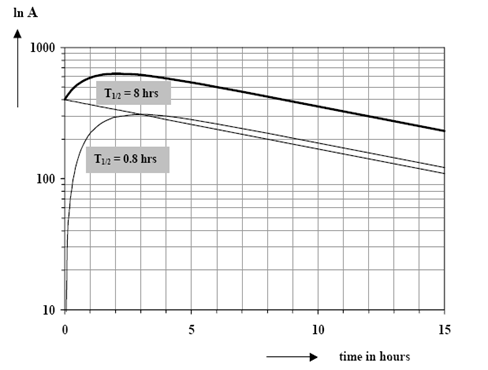
NO-EQUILIBRIUM
Here the half-life of the daughter nuclide is larger than that of the parent: λ1 ˃ λ2
The daughter activity is growing in the sample according to Eq. 7. Finally, after sufficiently long time, only daughter activity will be left, since the parent activity is disappearing at a higher rate:
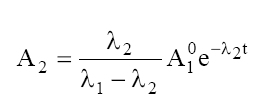
Difference between Radioactive Equilibrium and Chemical Equilibrium
Consider the radioactive decay series-
A …………> B……………> C
B is said to be in radioactive equilibrium with A if its rate of formation from A is equal to its rate of decay into C.
Consider a chemical reaction- A ↔ B
When the rate of forward reaction is equal to rate of backward reaction, the reaction is in Chemical Equilibrium or simply equilibrium.
Chemical equilibrium is affected by temperature, pressure and concentration but radioactive equilibrium independent of these.
Chemical equilibrium is a reversible process whereas radioactive equilibrium is an irreversible process.
Though we use Equilibrium term in case of radioactive decay series but actually it is a Steady State because the change in nuclear reaction is irreversible.
Branching Decay
Some radioactive nuclides exist that show more than one modes of decay.
e.g.
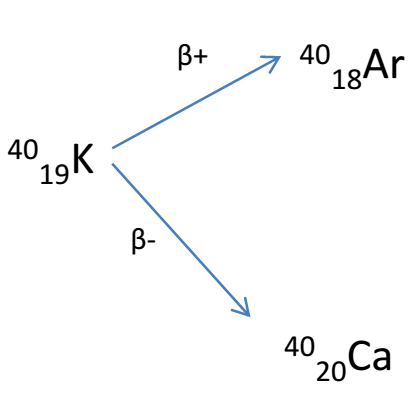
Each decay mode has its specific decay constant or half-life. The total decay is simply the sum of both single changes and is thus given by: λtotal = λ1 + λ2
Total half life: (1/t1/2)total = (1/t1/2)1 + (1/t1/2)2
