While the radiation propagates out from the nucleus, it interacts with other matter along its path. These interactions with external matter allow us to observe the radiation, and its effects, and to determine the nature of the transition inside the nucleus. This interaction of radiation with matter is also the cause of chemical, physical, and biological changes.
Except for neutrons all the radiation primarily interacts with bound electrons. For example, a silicon atom contains 14 electrons in a sphere with a radius of 0.12 nm that presents a geometrical cross section of 4.5 x 10-20 m2. The nucleus at the center of the sphere has a radius of 3.6 fm with a geometrical cross section of 4.1 X 10-29m2. The geometrical probability to strike the electrons in an atom is something like 9 orders of magnitude higher than that to strike the nucleus.
A scattered electron leaves the original atom and creates an ion pair. The interaction of a single particle of nuclear radiation can lead to tens or hundreds of thousands of ion pairs, and therefore, nuclear radiation is generally called ionizing radiation.
Classification of nuclear radiation
The overall scattering of the particle from an electron will be dominated by the mass and the charge on the particle. Considering the interaction of the radiation with electrons, we can divide nuclear radiation into four classes.
Charged Particles:
i. Protons, Heavy ions
ii. Electrons
Uncharged Particles:
i. Neutrons
ii. γ rays
Massive charged particles will tend to scatter the small mass electrons widely without losing much energy, while the collision of an electron with another electron will lead to energy sharing, and a photon can be scattered or even absorbed by a single bound electron.
Neutrons only interact very weakly with electrons through their small magnetic moment and predominately interact with nuclei. Usually, all of the interactions end up releasing energetic electrons.
Protons / Heavy ions
Nuclear reactions are expelled when the initial kinetic energy of the protons or heavy charged particle is lower than the Coulomb barrier. In fact, protons or heavy ions interact with an extremely large number of electrons, and we can examine the average behavior of the ions as they pass through the material.
Nuclear stopping power
When energetic charged ions move through the material on straight trajectories, giving up or losing kinetic energy through collisions with the atomic electrons of the material. The rate at which charged particles lose energy as they travel through a given material is called the stopping power of that material. The stopping power is made up of two parts, the electronic stopping power due to the interaction with the atomic electrons of the material and the nuclear stopping power.
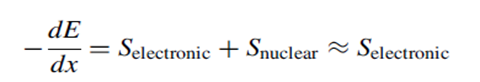
Because the electronic stopping power is always much larger than the nuclear stopping power. The minus sign on the rate indicates that the ions are losing kinetic energy. The stopping powers are functions of the mass, charge, and velocity of the ion, the atomic number, and the density of the medium.
Bohr ‘s classical formula is-
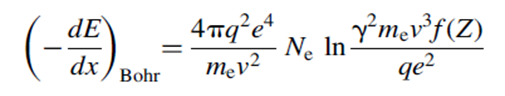
This expression has been superseded by the expression derived by Bethe and Bloch based on momentum transfer in a quantum mechanically correct formalism. Their expression with the expanded form of the electron number density is
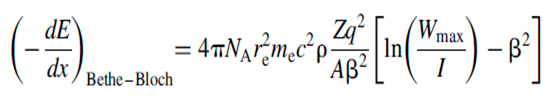
where,
NA is Avogadro’s number
re is the classical radius of the electron
r is the density of the stopping medium with atomic number, Z, mass number, A, and ionization potential, I
Wmax is the maximum energy transfer, encountered above.
The structure is very similar to the classical formula, but it includes an extra term in the logarithm.
Electrons
The passage of energetic electrons through matter is similar to that of heavy charged particles in that the Coulomb interaction plays a dominant role. However, three clear differences can be easily seen:
i. The incident electrons are generally relativistic particles
ii. The scattering is predominantly between identical particles and repulsive and
iii. The interactions with nuclei are attractive, and the direction of the electron can be dramatically changed, even reversed, in a collision with a heavy nucleus.
Besides this, a fraction of the kinetic energy is lost through the radiative process of bremsstrahlung. It is a German word meaning “braking radiation”. Bremsstrahlung is a general process in which electromagnetic radiation is produced by the acceleration of a charged particles, especially by electrons when it is deflected by another charged particle particularly, an atomic nucleus.
The scattering of electrons, particularly to large angles, corresponds to a classical acceleration that creates/ requires the emission of bremsstrahlung. Summarizing this overview of the possible interaction mechanisms for fast electrons in the material, we find that the rate of energy loss in a material is
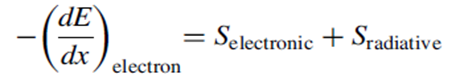
where the electronic stopping power is similar to the electronic interaction between
charged particles and electrons, whereas the radiative stopping power is specific to electrons. The electronic stopping power for electrons is written as:
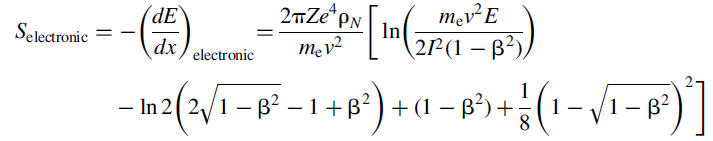
Using the same definitions as for the stopping power of heavy charged particles. On the other hand, the expression for the radiative stopping power is
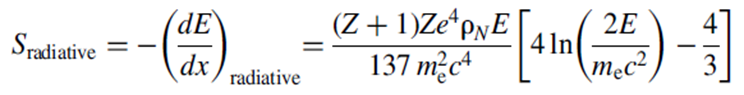
and given that b β≈ 1 contains an extra factor of ZE in the term in front of the parenthesis. With some algebra and for a typical electron energy, one can show that the ratio of the two contributions to the stopping power depends on the atomic number of the material, Z, and the electron kinetic energy E:
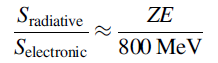
which indicates that the radiative contribution is only significant for large atomic
numbers (Z 80–90) and high electron energies (E 10–100 MeV). Typical β particles
from radioactive sources are emitted with only 1–10 MeV of kinetic energy, often much less, and the radiative contribution to the stopping power is very small.
The bremsstrahlung spectrum is smooth and continuous, ranging from zero energy up to the electron energy due to the random distribution of electron scattering angles.
Electromagnetic Radiation
while photons move through the material, they only interact or “scatter” in localized or discrete interactions, and they are not subject to the Coulomb or nuclear forces. As a result, when a beam of photons propagates through any material, the intensity of the beam will decrease as the photons that interact are removed, but the energy of all the noninteracting photons will remain constant.
The photons will interact in ways that predominantly release fast moving electrons, low-energy photons will interact only once and give rise to a single primary electron, energetic photons can interact several times and give rise to a few primary electrons. The most energetic photons can create a matter–antimatter pair of electrons that induce a flow of secondary electrons.
The energy of the noninteracting photons remains constant so that the probability that a photon will interact in a fixed thickness of material will also remain constant regardless of the photon energy. This leads immediately to an exponential attenuation of electromagnetic radiation that is called the Beer–Lambert law. The general expression for the attenuation of photons is-
I = I0e−µx
Where ,
I is transmitted intensities
I0 is incident intensities
x is the thickness, and
µ is an energy-dependent total linear absorption coefficient (depends on the nature of the material)
The mean free path of the photons in the material is simply λ = 1/µ and half-thickness is x1/2 = ln2/µ.
Problem Estimate the fraction of 1.0 MeV photons that will be transmitted through a lead absorber that is 5 cm thick (the thickness of “lead bricks” commonly used in radiation shields).
Solution The transmitted fraction is simply-
f =I/I0 = e−µx
Neutrons
Neutrons are the most penetrating radiation for the simple reason that their only significant interaction is with nuclei via the strong force. The insignificant interaction of neutrons with electrons through their magnetic dipole moment can be ignored.
Nuclei are very much smaller than atoms, and so the probability that a fast neutron will interact with (strike) a nucleus is very, very small. On the other hand, neutrons cause significant radiation damage because all of their interactions cause nuclear recoil and many lead to nuclear transmutations.
A neutron will move through material along a straight line with a constant energy until it encounters a nucleus and induces a nuclear reaction. Thus, neutron attenuation follows an exponential law similar to that for photons.
Written in terms of an energy-dependent attenuation length, µE we have I = I0e−µEx
where x is a linear dimension and I0 is the incident intensity. The attenuation length is the inverse of the mean free path, l, and is proportional to the total nuclear reaction cross section
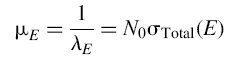
where N0 is a constant that gives the total number of nuclei per unit volume in the material. The total nuclear reaction cross section (σTotal) is a characteristic of each isotope in the absorbing material and has the dimensions of an area.
Cherenkov radiation
The light produced by charged particles when they pass through an optically transparent medium at speeds greater than the speed of light in that medium. Devices sensitive to this particular form of radiation, called Cherenkov detectors, have been used extensively to detect the presence of charged subatomic particles moving at high velocities.
Cherenkov radiation, when it is intense, appears as a weak bluish white glow in the pools of water shielding some nuclear reactors (Fig 1). The Cherenkov radiation in cases such as this is caused by electrons from the reactor traveling at speeds greater than the speed of light in water, which is 75 percent of the speed of light in a vacuum.
The energetic charged particle traveling through the medium displaces electrons in some of the atoms along its path. The electromagnetic radiation that is emitted by the displaced atomic electrons combines to form a strong electromagnetic wave. Soviet physicist Pavel A. Cherenkov first discovered this phenomenon in 1934.

